HOT
Trang chủ » Đề Thi » Đề Thi Toán

Đề thi chọn Học Sinh Giỏi Quốc gia môn Toán năm 2019 2020

By Thiên Minh | 29/12/2019

Mời các em cùng tham khảo bộ Đề thi chọn học sinh giỏi quốc gia môn Toán năm 2019 2020 vừa được các bạn học sinh hoàn thành vào sáng ngày 27 và 28/12/2019. Đề thi năm nay được đánh giá dễ thở và không gây sốc so với đề thi năm 2018.
Bài viết liên quan

Ghi chú: Tải "Tài liệu, Lời giải" có phí, bạn liên hệ qua Zalo: 0363072023 hoặc Facebook TẠI ĐÂY.

Đề thi chọn học sinh giỏi quốc gia môn Toán năm 2019 2020 đương nhiên sẽ có độ khó nhất định vì dành cho các em có học lực khá, giỏi trở lên, nội dung trong đề thi năm nay gồm có như: Tính Lim, tìm giá trị lớn nhất, dạng toán chứng minh...

Nội dung chi tiết 2 đề thi, mời các em theo dõi ngay dưới đây.

Nội dung câu hỏi số 3 trong ngày thi 27/12/2019

Cho dãy số (αn) xác định bởi α1 =  5.α2=13 và αn+2 = 5αn+1 - 6αn với mọi n ≥ 2.

a) Chứng minh rằng hai số hạng liên tiếp của dãy trên nguyên tốt cùng nhau.

b) Chứng minh rằng nếu P là ước nguyên tố của 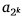de thi chon hoc sinh gioi quoc gia mon toan  thì p - 1 chia hết cho 2k+1 với mọi số tự nhiên k.

de thi chon hoc sinh gioi quoc gia mon toan

Trên đây là gợi ý đáp án và Đề thi chọn học sinh giỏi quốc gia môn Toán năm 2019 2020, có gọi ý đáp án. Chúc các em đạt điểm cao trong đợt thi vừa rồi. Các em tham khảo Đề thi chọn học sinh giỏi quốc gia môn Ngữ Văn năm 2019 2020 ở đây.

ĐG của bạn?

Donate: Ủng hộ website Giaitoan8.com thông qua STK: 0363072023 (MoMo hoặc NH TPBank).
Cảm ơn các bạn rất nhiều!

Bài viết liên quan
Từ khóa:

  • de thi chon hoc sinh gioi quoc gia mon toan

  • de thi chon hsg quoc gia mon toan

  • de thi mon toan chon hoc sinh gioi quoc gia

Danh mục Bài viết

Đọc nhiều

Bài mới