Bài tập tính khoảng cách từ điểm đến mặt phẳng có lời giải

Để tính được khoảng cách từ một điểm đến mặt phẳng, chúng ta cần nắm được các công thức toán học và hiểu được ý nghĩa của công thức đó, để khi áp dụng vào bài toán sẽ không lơ mơ vì chưa hiểu hết vấn đề.

Bài tập tính khoảng cách từ một điểm đến mặt phẳng.

I. Lý thuyết cần nắm được:

Cho $a$, $b$, $c$ là các số thực và ${a^2} + {b^2} + {c^2} > 0.$

Dạng 1: Khoảng cách từ một điểm đến một mặt phẳng.

Phương pháp: Điểm ${M_0}\left( {{x_0};{y_0};{z_0}} \right)$ và mặt phẳng $(\alpha ):ax + by + cz + d = 0.$

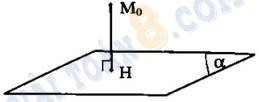
$d\left( {{M_0};(\alpha )} \right) = \frac{{\left| {a{x_0} + b{y_0} + c{z_0} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}.$

Hệ quả:
* ${M_0} \in (\alpha )$ $ \Leftrightarrow d\left( {{M_0};(\alpha )} \right) = 0.$
* $d\left( {{M_0};(\alpha )} \right) = {M_0}H$ với $\left\{ {\begin{array}{*{20}{l}}
{{M_0}H \bot (\alpha )}\\
{H \in (\alpha )}
\end{array}} \right..$
* Với mọi $M \in (\alpha ):$ $d\left( {{M_0};(\alpha )} \right) \le {M_0}M.$

Dạng 2: Khoảng cách giữa hai mặt phẳng song song.

Phương pháp: Cho hai mặt phẳng song song $(\alpha )$ và $(\beta )$, với $(\alpha ):ax + by + cz + d = 0$ và $(\beta ):ax + by + cz + D = 0$ $(d \ne D).$

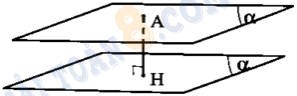
Lúc đó: $d((\alpha );(\beta ))$ $ = d(A;(\beta ))$ $ = \frac{{|d – D|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$ với $A \in (\alpha ).$

II. Bài tập minh họa.

Ví dụ 1

Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ $A(1;2;3)$ đến mặt phẳng $(Oxy).$
A. $d=1.$
B. $d=2.$
C. $d=3.$
D. $d = \sqrt 5 .$

Lời giải

Mặt phẳng $(Oxy)$ có phương trình: $z = 0.$
$ \Rightarrow d(A;(Oxy)) = \frac{{|3|}}{{\sqrt 1 }} = 3.$

Chọn đáp án C.

Ví dụ 2

Trong không gian với hệ tọa độ $Oxyz$, gọi $A’$ là điểm đối xứng của điểm $A(1;2;3)$ qua mặt phẳng $(Oxy).$ Tính độ dài đoạn thẳng $AA’.$
A. $4.$
B. $2.$
C. $3.$
D. $6.$

Lời giải

Mặt phẳng $(Oxy)$ có phương trình: $z = 0$ $ \Rightarrow d(A;(Oxy)) = \frac{{|3|}}{{\sqrt 1 }} = 3.$
Suy ra: $AA’ = 2d(A;(Oxy)) = 6.$

Chọn đáp án D.

Kết quả lưu ý: Với $\left( {{x_0};{y_0};{z_0}} \right)$ ta có:
$d(M;(Oxy)) = \left| {{z_0}} \right|.$
$d(M;(Oyz)) = \left| {{x_0}} \right|.$
$d(M;(Oxz)) = \left| {{y_0}} \right|.$

Ví dụ 3

Trong không gian với hệ tọa độ $Oxyz$, gọi $H$ là hình chiếu vuông góc của $A(1;2;-3)$ trên mặt phẳng $(Oxy).$ Tính diện tích $S$ tam giác $OHA.$
A. $S = \frac{{\sqrt {13} }}{2}.$
B. $S = \sqrt {10} .$
C. $S = \frac{{3\sqrt 5 }}{2}.$
D. $S = \frac{{5\sqrt {15} }}{2}.$

Lời giải

Ta có: $OA = \sqrt {14} $, $AH = d(A;(Oxy)) = 3.$
Tam giác $OHA$ vuông tại $H$ suy ra: $OH = \sqrt {O{A^2} – A{H^2}} = \sqrt 5 .$
Vậy $S = \frac{1}{2}AH.OH = \frac{{3\sqrt 5 }}{2}.$

Chọn đáp án C.

Ví dụ 4

Trong không gian với hệ tọa độ $Oxyz$, gọi $H$ là hình chiếu vuông góc của $A(1;2;-3)$ trên mặt phẳng $(Oxz).$ Tính diện tích $S$ tam giác $OHA.$
A. $S = \frac{{\sqrt {13} }}{2}.$
B. $S = \sqrt {10} .$
C. $S = \frac{{3\sqrt 5 }}{2}.$
D. $S = \frac{{5\sqrt {15} }}{2}.$

Lời giải

Ta có: $OA = \sqrt {14} $, $AH = d(A;(Oyz)) = 2.$
Tam giác $OHA$ vuông tại $H$ suy ra: $OH = \sqrt {O{A^2} – A{H^2}} = \sqrt {10} .$
Vậy $S = \frac{1}{2}AH.OH = \sqrt {10} .$

Chọn đáp án B.

Ví dụ 5

Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ $A(1;3;-2)$ đến mặt phẳng $(P):x + 2y – 2z + 1 = 0.$
A. $d=4.$
B. $d=2.$
C. $d=3.$
D. $d = \sqrt 5 .$

Lời giải

Ta có: $d(A;(P)) = \frac{{|1 + 6 + 4 + 1|}}{{\sqrt {{1^2} + {2^2} + {{( – 2)}^2}} }} = 4.$

Chọn đáp án A.

Ví dụ 6

Trong không gian với hệ tọa độ $Oxyz$, tính bán kính $R$ của mặt cầu tâm $A(1;3;2)$ và tiếp xúc với mặt phẳng $(P):x + 2y + 2z + 1 = 0.$
A. $d=4.$
B. $d=2.$
C. $d=3.$
D. $d = \sqrt 5 .$

Lời giải

Do mặt cầu tâm $A$ tiếp xúc với mặt phẳng $(P):$
$ \Leftrightarrow R = d(A;(P))$ $ = \frac{{|1 + 6 + 4 + 1|}}{{\sqrt {{1^2} + {2^2} + {{( – 2)}^2}} }} = 4.$

Chọn đáp án A.

Ví dụ 7

Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1;1;-2)$ và mặt phẳng $(P):2x+2y+z+1=0.$ Gọi $M$ là điểm bất kì thuộc $(P)$, tính độ dài nhỏ nhất của đoạn thẳng $AM.$
A. $2.$
B. $1.$
C. $\sqrt 2 .$
D. $\sqrt 3 .$

Lời giải

Gọi $H$ là hình chiếu vuông góc của $A$ trên $(P).$
Ta có: $AM \ge AH$ $ \Rightarrow A{M_{\min }} = AH = d(A;(P)) = 1.$

Chọn đáp án B.

Ví dụ 8

Trong không gian với hệ tọa độ $Oxyz$, cho điểm $K(1;1;0)$ và mặt phẳng $(\alpha ):x + y + z – 1 = 0.$ Gọi $(C)$ là đường tròn giao tuyến của mặt cầu tâm $K$, bán kính $R=2$ với mặt phẳng $(\alpha )$, tính diện tích $S$ của $(C).$
A. $S = \frac{{22\pi }}{3}.$
B. $S = \frac{{44\pi }}{3}.$
C. $S = \frac{{\sqrt {33} \pi }}{3}.$
D. $S = \frac{{11\pi }}{3}.$

Lời giải

Ta có: $d(K;(\alpha )) = \frac{{\sqrt 3 }}{3}.$ Gọi $r$ là bán kính đường tròn $(C)$, ta có: $r = \sqrt {{R^2} – {{[d(K;(\alpha ))]}^2}} = \frac{{\sqrt {33} }}{3}.$
Vậy $S = \pi {r^2} = \frac{{11\pi }}{3}.$

Chọn đáp án D.

Ví dụ 9

Trong không gian với hệ tọa độ $Oxyz$, cho điểm $P(2;1;3).$ Gọi $(C)$ là đường tròn giao tuyến của mặt cầu tâm $P$, bán kính $R=5$ với mặt phẳng $(Oxy)$, tính diện tích $S$ của $(C).$
A. $S = 24\pi .$
B. $S = 64\pi .$
C. $S = 16\pi .$
D. $S = 21\pi .$

Lời giải

Ta có: $d(P;(\alpha )) = 3.$
Gọi $r$ là bán kính đường tròn $(C)$, ta có:
$r = \sqrt {{R^2} – {{[d(P;(Oxy))]}^2}} = 4.$
Vậy $S = \pi {r^2} = 16\pi .$

Chọn đáp án C.

Ví dụ 10

Trong không gian với hệ tọa độ $Oxyz$, cho điểm $I( – 2;1;3).$ Gọi $(C)$ là đường tròn giao tuyến của mặt cầu tâm $I$, bán kính $R=5$ với mặt phẳng $(Oyz)$, tính diện tích $S$ của $(C).$
A. $S = 24\pi .$
B. $S = 64\pi .$
C. $S = 16\pi .$
D. $S = 21\pi .$

Lời giải

Ta có: $d(I;(\alpha )) = 2.$ Gọi $r$ là bán kính đường tròn $(C)$, ta có:
$r = \sqrt {{R^2} – {{[d(I;(Oyz))]}^2}} = \sqrt {21} .$
Vậy $S = \pi {r^2} = 21\pi .$

Chọn đáp án D.

Ví dụ 11

Trong không gian với hệ tọa độ $Oxyz$, cho điểm $F(-2;-1;5).$ Gọi $(C)$ là đường tròn giao tuyến của mặt cầu tâm $F$, bán kính $R=5$ với mặt phẳng $(Oxz)$, tính diện tích $S$ của $(C).$
A. $S = 24\pi .$
B. $S = 64\pi .$
C. $S = 16\pi .$
D. $S = 21\pi .$

Lời giải

Ta có: $d(F;(Oxz)) = 1.$ Gọi $r$ là bán kính đường tròn $(C)$, ta có:
$r = \sqrt {{R^2} – {{[d(F;(Oxz))]}^2}} = \sqrt {24} .$
Vậy $S = \pi {r^2} = 24\pi .$

Chọn đáp án A.

Trên đây là công thức và một số bài tập về tính khoảng cách từ điểm đến mặt phẳng có lời giải đi kèm. Chúc các em học tốt. Xem thêm Bài tập góc giữa hai mặt phẳng có lời giải ở đây.