Giải bài 1, 2, 3, 4, 5, 6 trang 79 sgk đại số 10
Cùng tham khảo tài liệu giải bài 1, 2, 3, 4, 5, 6 trang 79 sgk đại số 10, Bất đẳng thức dưới đây để hoàn thành bài tập được giao về nhà trong sách giáo khoa các bạn nha.
Ghi chú: Tải "Tài liệu, Lời giải" có phí, bạn liên hệ qua Zalo: 0363072023 hoặc Facebook TẠI ĐÂY.
Bài tập trong bài Bất đẳng thức trang 79 sách giáo khoa Đại số lớp 10 khá cơ bản, nó giúp chúng ta ôn lại kiến thức được học trong phần lý thuyết, nếu đang gặp khó khăn, thì tài liệu dưới đây sẽ giúp đỡ bạn rất nhiều đó.

Giải bài 1, 2, 3, 4, 5, 6 trang 79 sgk đại số 10, Bất đẳng thức
Giải bài tập Bất đẳng thức trang 79 sgk đại số 10
Giải bài 1 trang 79 SGK Đại Số 10:
a) chỉ đúng khi x > 0 (hay nói cách khác nếu x < 0 thì a) sai)
b) chỉ đúng khi x < 0
c) chỉ đúng khi x ≠ 0
d) đúng với mọi x.
Vậy khẳng định d là đúng với mọi giá trị của x.
Giải bài 2 trang 79 SGK Đại Số 10:

Giải bài 3 trang 79 SGK Đại Số 10:
a) Vì a, b, c là độ dài 3 cạnh của một tam giác
⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
⇒ a + c – b > 0 và a + b – c > 0
Ta có: (b – c)2 < a2
⇔ a2 – (b – c)2 > 0
⇔ (a – (b – c))(a + (b – c)) > 0
⇔ (a – b + c).(a + b – c) > 0 (Luôn đúng vì a + c – b > 0 và a + b – c > 0).
Vậy ta có (b – c)2 < a2 (1) (đpcm)
b) Chứng minh tương tự phần a) ta có :
( a – b)2 < c2 (2)
(c – a)2 < b2 (3)
Cộng ba bất đẳng thức (1), (2), (3) ta có:
(b – c)2 + (c – a)2 + (a – b)2 < a2 + b2 + c2
⇒ b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2 < a2 + b2 + c2
⇒ 2(a2 + b2 + c2) – 2(ab + bc + ca) < a2 + b2 + c2
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).
Giải bài 4 trang 79 SGK Đại Số 10:
Ta có: x3 + y3 ≥ x2y + xy2
⇔ (x3 + y3) – (x2y + xy2) ≥ 0
⇔ (x + y)(x2 – xy + y2) – xy(x + y) ≥ 0
⇔ (x + y)(x2 – xy + y2 – xy) ≥ 0
⇔ (x + y)(x2 – 2xy + y2) ≥ 0
⇔ (x + y)(x – y)2 ≥ 0 (Luôn đúng vì x + y ≥ 0 ; (x – y)2 ≥ 0)
Dấu « = » xảy ra khi (x – y)2 = 0 ⇔ x = y.
Giải bài 5 trang 79 SGK Đại Số 10:
Đặt t = √x (điều kiện t ≥ 0), khi đó
x4 – √x5 + x – √x + 1 = (√x)8 – (√x)5 + (√x)2 – (√x) + 1 = t8 – t5 + t2 – t + 1
Ta cần chứng minh : t8 – t5 + t2 – t + 1 > 0
Cách 1 (theo hướng dẫn ở đề bài).
+ Xét 0 ≤ t < 1 ⇒ t3 < 1 ⇒ 1 – t3 > 0 ; 1 – t > 0
t8 – t5 + t2 – t + 1 = t8 + (t2 – t5) + (1 – t)
= t8 + t2.(1 – t3) + (1 – t)
> 0 + 0 + 0 = 0
+ Xét t ≥ 1 ⇒ t3 ≥ 1 ⇒ t3 – 1 ≥ 0 và t – 1 ≥ 0.
t8 – t5 + t2 – t + 1 = t5.(t3 – 1) + t.(t – 1) + 1
≥ 0 + 0 + 1 > 0
Vậy với mọi t ≥ 0 thì t8 – t5 + t2 – t + 1 > 0 hay x4 – √x5 + x – √x + 1 > 0, ∀ x ≥ 0 (đpcm)
Cách 2:
2.(t8 – t5 + t2 – t + 1) = t8 + t8 – 2t5 + t2 + t2 – 2t + 1 + 1
= t8 + (t4 – t)2 + (t – 1)2 + 1.
≥ 0 + 0 + 0 + 1 = 1.
(Vì t8 ≥ 0 ; (t4 – t)2 ≥ 0; (t – 1)2 ≥ 0)
⇒ t8 – t5 + t2 – t + 1 ≥ 1/2 > 0 hay x4 – √x5 + x – √x + 1 > 0, ∀ x ≥ 0 (đpcm)
Giải bài 6 trang 79 SGK Đại Số 10:
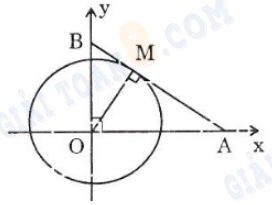
Gọi tiếp điểm của AB và đường tròn tâm O, bán kính 1 là M, ta có: OM ⊥ AB.
ΔOAB vuông tại O, có OM là đường cao nên MA.MB = MO2 = 1 (hằng số)
Áp dụng bất đẳng thức Cô-si ta có:
MA + MB ≥ 2√MA.MB = 2. √1 = 2
Dấu « = » xảy ra khi MA = MB = 1.
Khi đó OA = √(MA2 + MO2) = √2 ; OB = √(OM2 + MB2) = √2.
Mà A, B nằm trên tia Ox và Oy nên A(√2; 0); B(0; √2)
Vậy tọa độ là A(√2, 0) và B(0, √2).
Trong tài liệu sau, chúng ta sẽ tiếp tục giải bài Bất phương trình và hệ bất phương trình một ẩn nha!
Donate: Ủng hộ website Giaitoan8.com thông qua STK: 0363072023 (MoMo hoặc NH TPBank).
Cảm ơn các bạn rất nhiều!
- Giải bài 9.7 trang 86 SGK Toán 10 tập 2 Kết nối tri thức
- Giải bài 7 trang 32 SGK Toán 10 tập 2 Chân Trời Sáng Tạo
- Hệ thống bài tập trắc nghiệm xác suất sách Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức
- Giải bài 4.1 trang 50 SGK Toán 10 tập 1 Kết nối tri thức
- Cách giải bài 4.2 trang 50 SGK Toán 10 tập 1 Kết nối tri thức
giai bai 1 trang 79 sgk dai so 10
giai bai tap bat dang thuc trang 79 sgk dai so 10
giai bai tap trang 79 sgk dai so 10




















